A new search is underway.
Message boards :
News :
A new search is underway.
Message board moderation
| Author | Message |
|---|---|
 Eric Driver Eric DriverSend message Joined: 8 Jul 11 Posts: 1442 Credit: 920,287,689 RAC: 2,672,234 |
You may have noticed some new types of WUs for the decic search. We are taking a temporary detour to search for a special type of field. This search is exploratory in nature, and not a complete search (which would take way too long). Once this special field is found we will return to the search over {2,5}. The new search is for a particular A5 extension of Q(√421), ramified only at 2. Its existence is known from general theory applied to the 2-torsion points of the Jacobian of a special abelian surface. Due to its geometric origins, it has very limited ramification. On the other hand, it has non-solvable Galois group. This combination is difficult to find, and would provide a good example illustrating the general theory. Having the field explicitly would allow further computations to be done, such as computing the root discriminant of the Galois closure of the field, and computing Frobenius elements for many large primes. |
 Aurel AurelSend message Joined: 25 Feb 13 Posts: 216 Credit: 9,899,302 RAC: 0 |
Wow. That sounds amazing! (After I read the wikipedia sites about it) How many unit´s do you need? |
 Eric Driver Eric DriverSend message Joined: 8 Jul 11 Posts: 1442 Credit: 920,287,689 RAC: 2,672,234 |
Wow. That sounds amazing! (After I read the wikipedia sites about it) Not exactly sure. We are searching where the field is most likely to be found, slowly expanding the search as necessary. The first region we are searching requires about 50000 WUs. |
 Vitaly VitalySend message Joined: 5 Jan 13 Posts: 45 Credit: 62,573,354 RAC: 64,973 |
It is interesting. How many tasks have we already calculated in current search (798916 total tasks) |
 Eric Driver Eric DriverSend message Joined: 8 Jul 11 Posts: 1442 Credit: 920,287,689 RAC: 2,672,234 |
It is interesting. So we have narrowed the search space down to 12 congruence vectors; these have WU names of the form Qsqrt421_V[i]_DS3x[j]_Grp[k]of798916 where 1<=i<=4 and j comes from {2,5,8}. As you point out, each of these congruences is broken into 798916 pieces. Recall that a field can have many polynomial representatives, and they can occur anywhere in the search space. So to help improve our chances of finding a representative in a reasonable amount of time, we have randomized the order in which the 798916 WUs are generated. We also hop between the 12 sets, generating 50k units at a time. So far, we have crunched through about 350k WUs, and sadly we have not found it yet. But then again 350k is a small portion of the total 12x800k. I hope that helps explain the search a little better. |
 Vitaly VitalySend message Joined: 5 Jan 13 Posts: 45 Credit: 62,573,354 RAC: 64,973 |
Thank you Eric. Now the problem is much more clear. But I have one more question. From time to time "Number Field" tasks take 2-3 seconds to calculate (in particular, tasks for this project). Is it normal? |
 Eric Driver Eric DriverSend message Joined: 8 Jul 11 Posts: 1442 Credit: 920,287,689 RAC: 2,672,234 |
Thank you Eric. Yes, that is normal. We break the search space into equally sized pieces. Some of these pieces can finish quickly. |
 Eric Driver Eric DriverSend message Joined: 8 Jul 11 Posts: 1442 Credit: 920,287,689 RAC: 2,672,234 |
I just wanted to fill everyone in on the status of this special search. About a month ago we put it on hold while we reassessed the situation. We are now starting it back up again. It will be the same search but we are now looking in a different region of the search space. For those interested in the technical details, the previous guess was assuming that the prime above 2 had ramification Q1^4*Q2. Our new guess, which we believe to be a better guess, has ramification Q1^5. |
 Eric Driver Eric DriverSend message Joined: 8 Jul 11 Posts: 1442 Credit: 920,287,689 RAC: 2,672,234 |
We took a small break and are now returning back to this special search. One issue we had with these WUs was that the app was not check pointing frequently enough, in some cases several hours between check points. So we moved the check pointing block of code a couple layers deeper into the nested loops. This only applies to the GetDecics app - the new app version is 2.08 and it was uploaded several days ago. With the new app in place, we have generated new WUs for the special search. I didn't have time to run the WUs through my pre-filter, so you will notice some of them being very fast, however I have no way of knowing a priori what the proportion will be. If the percentage is sufficiently high, I will run future batches through the pre-filter. |
|
Send message Joined: 28 Oct 11 Posts: 182 Credit: 339,646,759 RAC: 235,583 |
There's still a small subset of tasks which don't checkpoint, or only checkpoint very rarely. This was a particularly extreme case: 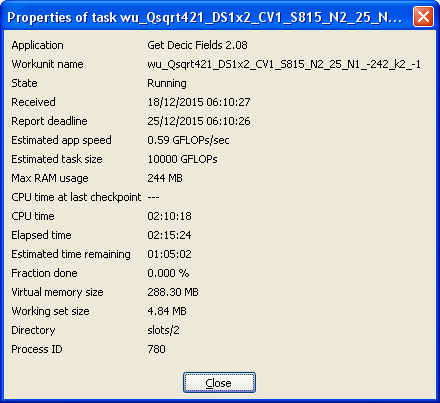 By coincidence, it finished and reported a few seconds after I'd taken that snapshot - task 13112010. They stick out, especially, on older BOINC clients, because they don't update the progress %age until the first checkpoint, and appear to be making no progress. Newer BOINC clients disguise this by inventing a 'pseudo-progress' report and displaying that instead - it probably reduces the number of unnecessary user aborts. This particular task was unusual in not checkpointing at all. There seems to be a slightly larger sub-population which checkpoint just twice: they can be spotted by spending a non-trivial amount of time at precisely 40.000% and 80.000% I doubt either type is a significant problem (they do complete and validate), but might be worth consideration at the next revision. |
 Eric Driver Eric DriverSend message Joined: 8 Jul 11 Posts: 1442 Credit: 920,287,689 RAC: 2,672,234 |
This is actually expected. I can elaborate. After moving the checkpointing deeper into the loop structure, it was then easy to extend the WU format to include ranges for those inner loops. It turned out this was necessary for this special test (discovered after 2 weeks of testing and the reason for the hiatus). In the slowest regions I ended up making WUs that used a single value for the innermost checkpointing loop - this reduced run times from about 12 hours to 2 hours but then only checkpointed once at the end of the search. I could move checkpointing even deeper into the looping, but I am hesitant to do that. There is a slight computational overhead to doing that, which may impact the standard decic search (recall they use the same app). One other thing I should mention, the cases that jump by steps of 20% are ones that set values 1 level above the innermost loop. These WUs loop completely over the innermost checkpointing loop of which there are 5 values (for the cases I have seen so far), some of which go really fast so may appear to jump by 40%. You can tell what kind of case you have by the WU name which contains the search values for the various indices. CV stands for congruence vector. Other loop indices are N2, N1, k2. If there is a value for k2 then it will be one of those that appears to not checkpoint. I hope that explanation is not too confusing. Don't hesitate to ask if you have any questions. |
 Eric Driver Eric DriverSend message Joined: 8 Jul 11 Posts: 1442 Credit: 920,287,689 RAC: 2,672,234 |
We are modifying our search strategy on this special search. The previous strategy searched about 20% of the space with a discriminant bound reduced by 81.5% (now you know what the S815 meant in the WU names). This search revealed regions where an above average number of polynomials passed the first set of tests but failed to find the field of interest. The new strategy is to focus on these particular regions but use the full bound. I have also been doing some timing analysis of the collected results and using that to fine tune the work unit generator so that WUs have better run times (not so long). Also on my list is to add a table to the Batch status page for the Qsqrt cases. |
 Eric Driver Eric DriverSend message Joined: 8 Jul 11 Posts: 1442 Credit: 920,287,689 RAC: 2,672,234 |
As promised, the batch status page has been updated to include the new Qsqrt421 batches. Also, the old completed bounded tables have been archived and removed from the page. |
 Eric Driver Eric DriverSend message Joined: 8 Jul 11 Posts: 1442 Credit: 920,287,689 RAC: 2,672,234 |
You may have noticed some new types of WUs for the decic search. We are taking a temporary detour to search for a special type of field. This search is exploratory in nature, and not a complete search (which would take way too long). Once this special field is found we will return to the search over {2,5}. I am happy to report that the hypothesized field has finally been found! Further analysis is now being done on the field to gain insight into the corresponding abelian surface. I will report back any interesting developments that come from this. Thanks goes to all you volunteers who made this discovery possible. |
Copyright © 2026 Arizona State University